PCA降维(信号处理领域也叫KLT变换)

PCA 与 Linear Regression 的区别：

1. PCA衡量的是orthogonal distance, 而linear regression是所有x点对应的真实值y=g(x)与估计值f(x)之间的vertical distance距离
2. more general 的解释：PCA中为的是寻找一个surface，将各feature{x1,x2,…,xn}投影到这个surface后使得各点间variance最大（跟y没有关系，是寻找最能够表现这些feature的一个平面）；而Linear Regression是给出{x1,x2,…,xn}，希望根据x去预测y，所以进行回归。

算法：

1. 计算各个feature的平均值，计μj ;（Xj(i)表示第i个样本的第j维特征的value）
   μj = Σm Xj(i)/m
2. 将每一个feature scaling：将在不同scale上的feature进行归一化；
3. 将特征进行mean normalization
   令Xj(i)= (Xj(i)-μj)/sj
4. 求n×n的协方差矩阵Σ：
   
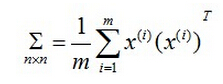
5. 根据SVD求取特征值和特征向量：
   [U,S,V] = SVD（Σ）
6. 按特征值从大到小排列，重新组织U
   如果使用matlab的svd求得特征值，就可以直接跳过这步了，因为该函数返回值中，奇异值在S的对角线上按照降序排列。否则的话应进行排序，并按照该次序找到对应的特征向量重新排列。
7. 选择k个分量
   按照第五、六步中讲的svd过后，我们得到了一个n×n的矩阵Σ和U，这时，我们就需要从U中选出k个最重要的分量；即选择前k个特征向量，即为Ureduce,
   该矩阵大小为n×k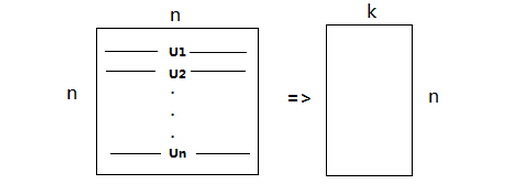
   
   这样对于一个n维向量x，就可以降维到k维向量z了：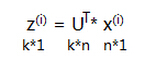
   

从压缩数据中恢复原数据

我们已经知道，可以根据z(i) = Ureduce’× x(i) 将n维向量x降维到k维向量z，那么有时我们需要恢复n维向量，怎么做呢？
由于Ureduce是正交矩阵（下面Ureduce简记为U），即U’ = U-1, 所以
xapprox = (U’)-1×z = (U-1)-1×z = Uz
(PS：这里的逆操作为伪逆操作)
注意：这里恢复出的xapprox并不是原先的x，而是向量x的近似值。

怎样决定降维个数/主成分个数

首先从一个general一点的思路去想呢，我们是希望，选出主成分之后进行数据分析，不会造成大量特征的丢失，也就是说可以用下式的error ratio表示经过压缩后的性能如何。

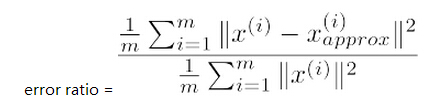
然后呢，我们定义一个threshold（10% for example）,如果error ratio<threshold，说明这样选取主成分是可以接受的，从数学上可以证明，也可以用下式进行k的合理选取

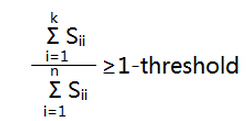
Tips:

1. PCA降维并不能阻止训练结果的过拟合，这个效果往往很小，阻止过拟合还是需要添加规则项。

参考：

Stanford机器学习—-第十讲. 数据降维
UFLDL教程