网络模型训练阶段对于欠拟合和过拟合的关系？

1. 任何一个最小二乘均方差cost function都可以表示为bias方和variance和一个噪声的叠加，其中bias值得是最终数据集的预测结果均值和期望结果的偏差，而variance指的是最终所有样本的预测结果，这些结果的方差。我们训练最终需要的效果是尽可能的使bias和variance都很小。
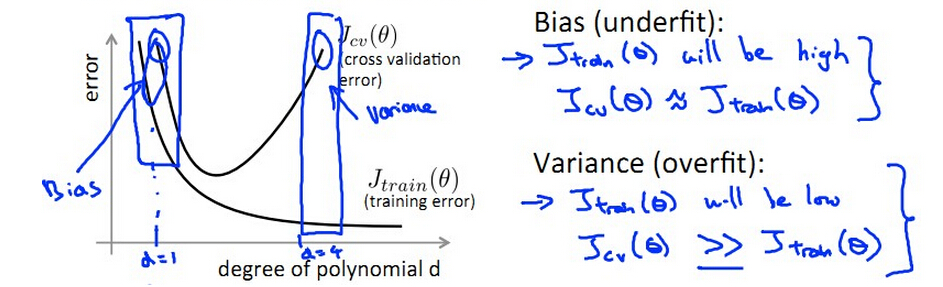
2. 欠拟合的情况下，训练集误差大，交叉验证误差大，测试误差大，λ太大导致underfit，产生bias，J(train) ≈ J(cv)，此时bias大，但是variance小。
3. 过拟合的情况下，训练集误差小，交叉验证误差大，测试误差大λ太小而导致overfit，产生variance，J(train)<<J(cv) ，此时bias小，但是variance大。
4. 在欠拟合的情况下，增加训练样本是不能提高预测效果的，只有在过拟合的情况下，增加训练样本，才能使variance更小。
   

基本神经网络算法：

1. 随机初始化权重；
2. Repeat
   前向传播计算实际输出；
   根据误差和残差，反向传播更新权重

残差和权重更新公式：

最后一层：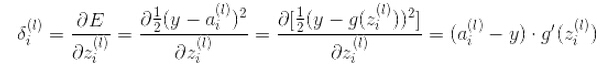
中间层
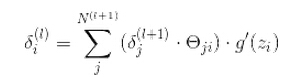（j代表层节点个数）


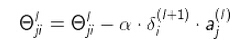
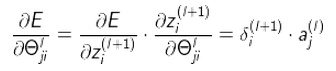
换句话说, 对于每一层来说，δ分量都等于后面一层所有的δ加权和，其中权值就是参数Θ和后一层的激活函数的导数之积。

参考：

bias和variance
Stanford机器学习—-第六讲. 怎样选择机器学习方法、系统
Back Propagation算法推导过程
神经网络的学习 Neural Networks learning
UFLDL教程