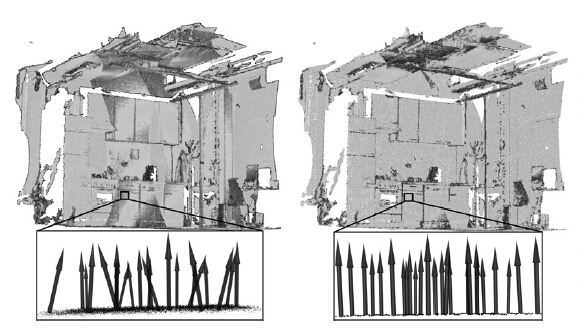
MLS是点云领域内比较重要，并且也是用的比较多的平滑方法，Pcl封装了MLS的函数并且可以利用MLS来估算点云的法向，在此基础上，Rusu曾提出更为鲁棒的RMLS算法，可以抑制在sharp边缘处被平滑成光滑的曲面。

普通MLS算法

原始点云c 生成的曲面s
遍历c中每一点x，并且获取p点周围的邻域点集
拟合函数f(x)=∑ p(x)a(x)
P(x)为设定好的阶次函数，a(x)为与x有关的函数
J=∑ w（x）(f(x)-y) 求取最小，y为c中x对应的y值，f(x)为拟合的值，w为权重函数

依据此获取全局的a（x）函数
最终将所有的c中的x点拉至拟合的曲面s上，最终满足下式

Rusu的RMLS算法

和普通mls不同的是，在进行逼近拟合之前，需要进行参考面拟合，为了剔除外点，05年采用的是带权重的RANSAC进行参考面拟合，07年借鉴了前人的算法，采用了极大似然进行参考面的估计，之后剔除了外点，只用参考面上的进行mls拟合。
这样在边缘地带可以防止2个平面交界处平滑成曲面。

附：MLS的参考

原创博文

转载请注明出处