原创————SDF和marching cubes算法
SDF三维表达仅仅包含对三维数据的表达,而并不是面片最终的表达。SDF是一种隐函数,如果需要对最终面片进行表达,需要通过marching cubes 算法提取各个体素的面片。
基本SDF框架:
- 在三维空间构造体素,并对体素初始化为空;
- 将三维数据分配到体素中;
- 对体素各个顶点进行刷新:通过视点到该顶点的射线和该点附近的面片交与一点,顶点到该点的距离即为该点的D(x),w(x)通过计算该点周围面片定点的法向量和这条射线进行加权求得;
- 当心的数据获取后,将新数据的SDF和原始的SDF加权融合,即新的体素中顶点的d(x)和w(x);
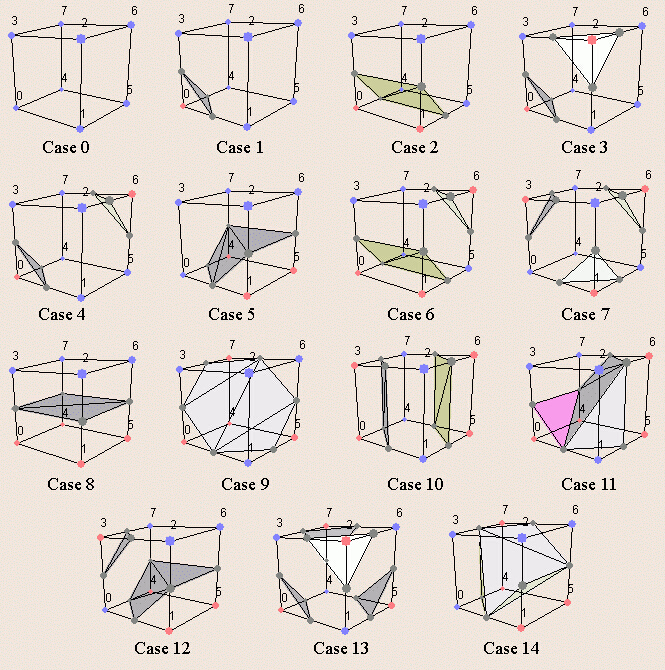
- 最终通过marching cubes 提取面片输出。
填补空洞的SDF框架:
- 在三维空间构造体素,并对体素初始化为unseen标志,体素顶点的D(x)设为最大Dmax;
- 将三维数据分配到体素中,分配的体素标志为varying;
- 对体素各个顶点进行刷新:通过视点到该顶点的射线和该点附近的面片交与一点,顶点到该点的距离即为该点的D(x),w(x)通过计算该点周围面片定点的法向量和这条射线进行加权求得;
- 对体素的状态进行刷新:从该交点到视点的直线所经过的体素更新标志为empty,顶点D(x)设为最小Dmin;
- 当心的数据获取后,将新数据的SDF和原始的SDF加权融合,即新的体素中顶点的d(x)和w(x),并更新体素的状态;
- 最终通过marching cubes 提取面片输出。
http://users.polytech.unice.fr/~lingrand/MarchingCubes/algo.html#msAmb 给出了marching cubes的官网,可以提取最终面片 。
Tips:
1.采用什么数据结构,一个体素8个顶点,相邻的体素会有公用顶点,数据结构不仅减少内存,更对顶点状态的更新有帮助,仅通过一次更改即可对所有体素的该顶点状态更新;
2.Marching cubes存在奇异性,程序上需要对奇异状态的cubes进行互补求解,得到更好的面片。

